Maxime Clusel

Some previous results:
-
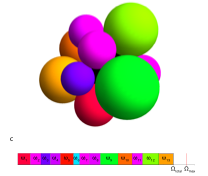
 A granocentric model for polydisperse packing of spheres
A granocentric model for polydisperse packing of spheres
with E.I. Corwin (U. Oregon), A.E.O. Siemens (Leiden University) and J. Brujic (New York University).
We propose a statistical model for the random packing of frictionless polydisperse spheres in which the complexity of the global packing is distilled into a local stochastic process. We simplify the problem by considering the “granocentric” point of view of a single particle in the bulk, thereby reducing random packing to the assembly of nearest neighbours, followed by a random choice of contacts among them. The model is based on only two parameters, the available solid angle around each particle and the ratio of contacts to neighbors, which are both directly obtainable from experiments or simulations. As a result, the model analytically predicts the microscopic distributions of nearest neighbours and contacts, the local density fluctuations as well as the global density of the packing. We find that this granocentric view captures the essential properties of the polydisperse emulsion packing.
Talk on packing of polydisperse spheres
-
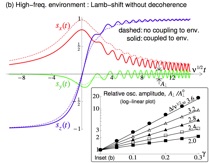
 Effects of a non-Markovian environment on Landau-Zeener transition
Effects of a non-Markovian environment on Landau-Zeener transition
with R.S. Whitney (LPMMC, Grenoble) and T. Ziman (ILL, Grenoble).
We consider sweeping a system through a Landau-Zener avoided crossing, when that system is also coupled to an environment or noise. Unsurprisingly, we find that decoherence suppresses the coherent oscillations of quantum superpositions of system states, as superpositions decohere into mixed states. However, we also find an effect we call “Lamb-assisted coherent oscillations,” in which a Lamb shift exponentially enhances the coherent-oscillation amplitude. This dominates for high-frequency environments such as super-Ohmic environments, where the coherent oscillations can grow exponentially as either the environment coupling or temperature are increased.
Colloquium on quantum open systems -
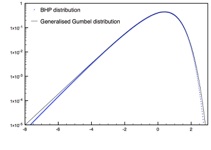
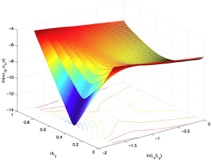
 Extreme value statistics and sums of correlated random variables
Extreme value statistics and sums of correlated random variables
with E. Bertin (CNRS, ENS Lyon)
We show that generalised extreme value statistics -the statistics of the k-th largest value among a large set of random variables- can be mapped onto a problem of random sums. This allows us to identify classes of non-identical and (generally) correlated random variables with a sum distributed according to one of the three (k-dependent) asymptotic distributions of extreme value statistics, namely the Gumbel, Frechet and Weibull distributions. These classes, as well as the limit distributions, are naturally extended to real values of k, thus providing a clear interpretation to the onset of Gumbel distributions with non-integer index k in the statistics of global observables. This is one of the very few known generalisations of the central limit theorem to non-independent random variables. Finally, in the context of a simple physical model, we relate the index k to the ratio of the correlation length to the system size, which remains finite in strongly correlated systems.
Talk on extreme value statistics and sums of correlated variables
Talk on large scale fluctuations in correlated systems
Talk on protein mechanical properties at the single molecule level
-
 Ising models and Grassmann algebra
Ising models and Grassmann algebra
with J.-Y. Fortin (CNRS IJL, Nancy) et V.N. Plechko (JINR Dubna, Russia).
We develop an alternative method to that proposed by McCoy and Wu to obtain some exact results for the 2D Ising model with a general boundary magnetic field and for a finite size system. This method is a generalization of ideas from Plechko presented for the 2D Ising model in zero field, based on the representation of the Ising model using a Grassmann algebra. A Gaussian 1D action is obtained for a general configuration of the boundary magnetic field. When the magnetic field is homogeneous, we check that our results are in agreement with McCoy and Wu's previous work. This 1D action is used to compute in an efficient way the free energy in the special case of inhomogeneous boundary magnetic field. This method is useful to obtain new exact results for interesting boundary problems, such as wetting transitions. In this context we proposed an exact study of a first-order transition induced by an inhomogeneous boundary magnetic field in the 2D Ising model. From a previous analysis of the interfacial free energy in the discrete case, we identify, using an asymptotic expansion in the thermodynamic limit, the line of transition that separates the regime where the interface is localized near the boundary from the one where it is propagating inside the bulk. In particular, the transition line has a strong dependence on the aspect ratio of the lattice.
Talk on Ising model and Grassmann algebra
Current research interests:
-
 Quantum stochastic thermodynamics
Quantum stochastic thermodynamics
with P. Degiovanni, I. Frérot, B. Roussel (ENS Lyon) A. Auffèves, C. Élouard (I. Néel, Grenoble).
Collaborations: B. Huard (ENS Paris)
Progress has been made during the last decades in the development of a statistical theory for classical out-of equilibrium system. In addition to celebrated fluctuation theorems, stochastic thermodynamic now provides both a nice unifying theoretical framework and a useful way for studying these systems experimentally. It was for instance at the heart of the first experimental verification of Landauer’s principle. This success in understanding classical systems drew interest in similar problems for out-of-equilibrium quantum systems. A set of various fluctuation relations have then been obtained. Severe issues however appeared in the very definition of thermodynamic quantities for quantum systems, so that a unified framework for driven out-of-equilibrium quantum open system is not yet available. We propose to fill this gap by constructing a quantum stochastic thermodynamics based on a quantum trajectory description of quantum open systems. Introduced in the context of quantum optics, these trajectories have recently become relevant physical objects thanks to several experimental breakthrough.
This framework allows for definitions at the single trajectory level of basic thermodynamic quantities such as heat transfer, work and entropy. Using this approach we identified quantum contributions to work and heat transfer. In particular we find a contribution of quantum coherence to heat that can be interpreted as the thermal imprint Schrodinger’s cat leaves in the environment after its death.
This formalism can then be used to obtained “central” fluctuation theorems, from which follow more practical fluctuation relations such as Jarzynski and Crooks fluctuation theorems for instance. This framework will be applied to have a thermodynamic point of view on simple processes such as a Landauer erasing protocol or the Landau Zener transition.
We are now working in collaboration with experimentalists to explore the applicability of such a formalism to actual experimental protocols.
-
 Dense packing of active particles
Dense packing of active particles -
 Extreme value statistics of correlated random variables
Extreme value statistics of correlated random variables
with J.-Y. Fortin (IJL, Nancy)